一种高性能的正方形识别系统
前言
最近完成了一个计算机视觉算法,算是一个基于角点检测的正方形识别系统。这个算法从最初的想法到最终的实现,经历了很多有趣的技术挑战和优化过程。
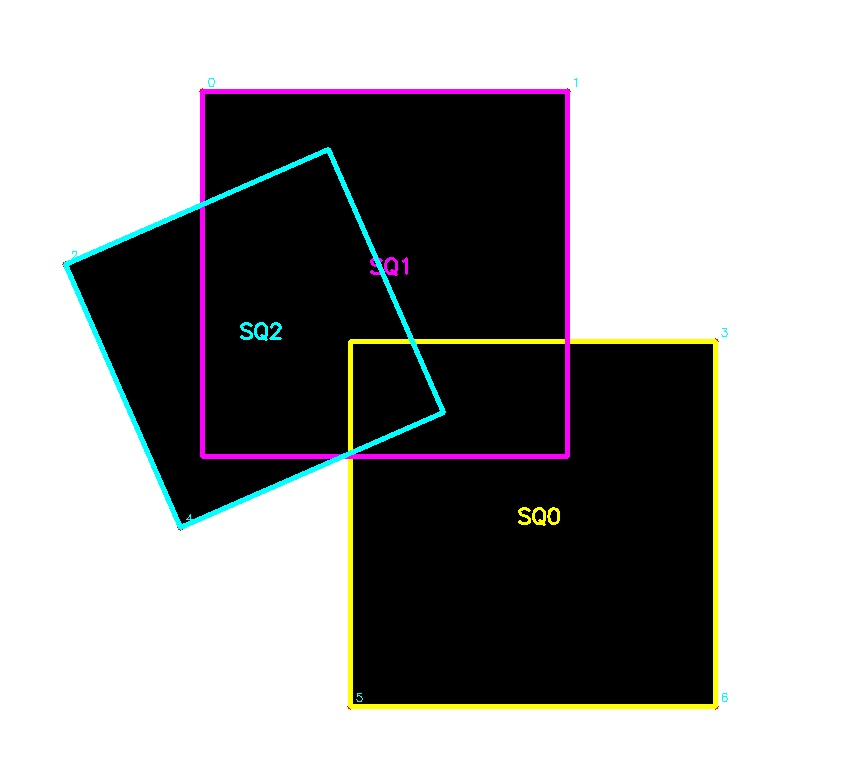
首先简要概述一下问题,一个白色背景上有若干黑色大小不一,角度不同且可能重叠的正方形,保证每个正方形有两个可见的角,需要识别出所有的正方形。下面是一个例子:

1. 算法设计
1.1 图像预处理
首先,我们需要将输入图像转换成算法易于处理的格式。这里我用了OTSU二值化处理:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| def load_image_from_file(self, image_path: str, binarize: bool = True, threshold: int = 127):
"""
为什么要二值化?
1. 简化计算:只需要区分黑白两种状态
2. 减少噪声:去除灰度变化带来的干扰
3. 提高速度:布尔运算比数值计算更快
"""
loaded_image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
if binarize:
if threshold == -1:
threshold_value, binary_image = cv2.threshold(
loaded_image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
print(f"OTSU算法选择的阈值: {threshold_value:.1f}")
else:
_, binary_image = cv2.threshold(loaded_image, threshold, 255, cv2.THRESH_BINARY)
self.image = binary_image
|
这里提供了三种二值化选项,是因为不同的应用场景需要不同的处理策略。OTSU算法特别适合光照不均匀的情况,而固定阈值则在工业环境中更稳定。
1.2 高效找角点
由于这个图中都是正方形,理论上找出所有直角,就可以尝试解决问题。这里我使用了一种专门面向这个问题的思路。思考对一个直角点进行范围取样之后的结果:
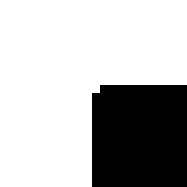
容易发现,如果在一个较大范围内,计算黑色像素占比,那么它应该比较接近25%,当然取样面积太小的话,因为边缘误差可能导致黑色像素比例相比25%偏多。
现在我们的目标就是,如何快速计算一个区域内黑色像素点的数量。
1.2.1 构建前缀和矩阵
这是整个系统最关键的优化点。让我详细解释一下为什么要用前缀和:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| def build_prefix_sum_matrix(self):
"""
前缀和矩阵的核心思想:
如果我们要频繁计算矩形区域内的黑色像素数量,
传统方法需要O(W×H)的时间复杂度,太慢了!
前缀和的巧妙之处:
prefix_sum[y][x] = 从(0,0)到(x,y)矩形内所有黑色像素的总数
"""
height, width = self.image.shape
self.prefix_sum = np.zeros((height + 1, width + 1), dtype=np.int32)
print("构建前缀和矩阵...")
for y in range(1, height + 1):
for x in range(1, width + 1):
is_black = 1 if self.image[y-1, x-1] == 0 else 0
self.prefix_sum[y, x] = (is_black +
self.prefix_sum[y-1, x] +
self.prefix_sum[y, x-1] -
self.prefix_sum[y-1, x-1])
def get_black_pixel_count_in_rect(self, x1: int, y1: int, x2: int, y2: int) -> int:
"""
有了前缀和矩阵,计算任意矩形区域的黑色像素数量只需要O(1)时间!
这是二维前缀和的经典应用
"""
return (self.prefix_sum[y2, x2] -
self.prefix_sum[y1, x2] -
self.prefix_sum[y2, x1] +
self.prefix_sum[y1, x1])
|
为什么这么设计?
我举个例子:假设我们要检测1000×1000的图像中的所有角点,每个角点都需要计算周围20×20区域的黑色像素比例。
- 传统方法:每次计算需要400次像素检查,总计需要1000×1000×400
= 4亿次操作
- 前缀和方法:构建一次前缀和(100万次操作),之后每次查询只需要4次运算,总计约100万次操作
效率提升了400倍。
1.3 角点多层过滤
由于现实世界的图像往往不完美,我设计了一个多层过滤系统:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| def detect_all_outer_corners(self):
"""
通过多层过滤,逐步提高候选点的质量
"""
for y in range(edge_threshold, self.image_size[1] - edge_threshold):
for x in range(edge_threshold, self.image_size[0] - edge_threshold):
if not self.is_black_pixel(x, y):
continue
if not self.is_edge_pixel(x, y):
continue
corner_black_ratio = self.calculate_black_pixel_ratio(x, y, radius=10)
if corner_black_ratio < 0.1 or corner_black_ratio > 0.4:
continue
try:
assist_points = self.find_two_edge_assist_points(x, y, radius=10)
if assist_points and len(assist_points) == 2:
all_corners.append(((x, y), assist_points[0], assist_points[1]))
except:
continue
|
设计思路解析:
- 边缘像素检测:首先角点肯定要求是边缘上的点
- 黑色比例过滤:0.1-0.4的范围是经过大量实验确定的最佳区间
- 辅助点寻找:通过寻找90度夹角的边缘点来验证这是一个真正的角点,同时也可以记录这个角两条边的方向。
为什么这样设计?
实际图像中的角点往往不是完美的90度角,可能是圆角、磨损的角或者有噪声的角。传统方法会漏掉这些”不完美”的角点,而我的方法通过统计学的思路,只要该点具有角点的统计特征就接受它。
具体边缘检测的思路也很简单,考虑周围八个像素就可以了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| def is_edge_pixel(self, x: int, y: int) -> bool:
"""
我的边缘检测思路:
不追求完美的边缘,而是寻找"有意义"的边缘
一个像素如果是黑色,但周围8个邻居不全是黑色,
那它就是边缘像素
"""
if not self.is_black_pixel(x, y):
return False
neighbors = [(-1, -1), (-1, 0), (-1, 1),
(0, -1), (0, 1),
(1, -1), (1, 0), (1, 1)]
black_neighbors = 0
valid_neighbors = 0
for dx, dy in neighbors:
check_x, check_y = x + dx, y + dy
if 0 <= check_x < self.image_size[0] and 0 <= check_y < self.image_size[1]:
valid_neighbors += 1
if self.is_black_pixel(check_x, check_y):
black_neighbors += 1
return valid_neighbors > black_neighbors
|
在实际程序中,这里也可以引入多线程优化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| def detect_all_outer_corners(self):
"""
多线程设计思路:
将图像水平分割成两部分,两个线程并行处理
这样可以充分利用多核CPU的优势
"""
start_y = edge_threshold
end_y = self.image_size[1] - edge_threshold
mid_y = (start_y + end_y) // 2
corners_thread1 = []
corners_thread2 = []
lock = threading.Lock()
def scan_upper_half():
"""线程1负责上半部分"""
local_corners = []
for y in range(start_y, mid_y):
with lock:
corners_thread1.extend(local_corners)
def scan_lower_half():
"""线程2负责下半部分"""
pass
thread1 = threading.Thread(target=scan_upper_half)
thread2 = threading.Thread(target=scan_lower_half)
thread1.start()
thread2.start()
thread1.join()
thread2.join()
|
为什么选择水平分割?
我尝试过垂直分割和棋盘式分割,但发现水平分割效果最好,原因是: 1.
图像的行是连续存储的,缓存友好 2. 避免了复杂的边界处理 3.
负载均衡效果好(每个线程处理相同的行数)
1.4 正方形重建
如何从检测到的角点重建出完整的正方形?我设计了一个多策略的方案:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| def reconstruct_squares(self, corners):
"""
重建策略的优先级设计:
4角点 > 3角点 > 2角点
为什么这样排序?
- 4角点:信息最完整,几乎不会出错
- 3角点:信息充足,可以通过几何推理得到第4个点
- 2角点:信息最少,但仍然可以通过共线和平行关系推理
"""
squares_4_corners = self.find_squares_with_4_corners(corners, used_corners)
squares_3_corners = self.find_squares_with_3_corners(corners, used_corners)
squares_2_corners = self.find_squares_with_2_corners(corners, used_corners)
|
让我详细解释每种策略:
策略一:4角点验证
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| def are_4_points_square(self, points, tolerance=5.0):
"""
如何验证4个点是否构成正方形?
1. 计算所有6条边(4条边+2条对角线)
2. 前4条应该相等(边长)
3. 后2条应该相等(对角线)
4. 对角线 = 边长 × √2
"""
distances = []
for i in range(4):
for j in range(i + 1, 4):
dist = np.sqrt((points[i][0] - points[j][0])**2 +
(points[i][1] - points[j][1])**2)
distances.append(dist)
distances.sort()
side_length = distances[0]
diagonal_length = distances[4]
for i in range(4):
if abs(distances[i] - side_length) > tolerance:
return False
expected_diagonal = side_length * np.sqrt(2)
if abs(diagonal_length - expected_diagonal) > tolerance:
return False
return True
|
策略二:3角点推理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| def calculate_fourth_corner(self, three_points):
"""
从3个点推理第4个点的数学原理:
在正方形ABCD中,如果知道A、B、C三点,
那么第四个点D = A + C - B(向量运算)
但是我们不知道哪三个点的对应关系,所以要尝试所有可能的组合
"""
for i in range(3):
for j in range(3):
if i == j:
continue
p1, p2, p3 = three_points[i], three_points[j], three_points[(set(range(3)) - {i, j}).pop()]
p4 = (p1[0] + p3[0] - p2[0], p1[1] + p3[1] - p2[1])
if self.are_4_points_square([p1, p2, p3, p4]):
return p4
return None
|
策略三:2角点智能构建
这是最复杂的情况,需要区分相邻角点和对角角点:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| def find_squares_with_2_corners(self, corners, used_corners):
"""
2角点重建的核心思路:
1. 判断两个角点是相邻还是对角关系
2. 相邻:利用共线边和平行边的关系
3. 对角:利用直线交点计算其他两个角点
"""
for i in range(len(corners)):
corner1 = corners[i]
for j in range(i + 1, len(corners)):
corner2 = corners[j]
if self.are_adjacent_corners(corner1, corner2):
square = self.build_square_from_adjacent_corners(corner1, corner2)
if square and self.validate_square(square):
squares.append(square)
else:
square = self.build_square_from_diagonal_corners(corner1, corner2)
if square and self.validate_square(square):
squares.append(square)
|
1.5 结果去重
在检测过程中,同一个正方形可能被多种策略检测到,需要智能的去重机制,这里的重叠度计算基于两个正方形中心位置的差异:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| def remove_duplicate_squares(self, squares, overlap_threshold=0.95):
"""
去重策略的核心思想:
1. 计算几何重叠度
2. 比较黑色像素质量
3. 考虑旋转角度差异
4. 保留最优结果
"""
if len(squares) <= 1:
return squares
square_ratios = []
for square in squares:
ratio = self.calculate_square_black_ratio(square)
square_ratios.append(ratio)
keep_flags = [True] * len(squares)
for i in range(len(squares)):
if not keep_flags[i]:
continue
for j in range(i + 1, len(squares)):
if not keep_flags[j]:
continue
overlap = calculate_square_overlap(squares[i], squares[j])
if overlap > overlap_threshold:
if self.are_squares_different_rotation(squares[i], squares[j]):
continue
if square_ratios[i] >= square_ratios[j]:
keep_flags[j] = False
else:
keep_flags[i] = False
break
return [squares[i] for i in range(len(squares)) if keep_flags[i]]
|
在考虑旋转差异的时候,必须考虑到正方形的对称性:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| def calculate_square_rotation_angle(square):
"""
由于正方形的90度对称性,映射到[0, 90)
"""
if len(square) != 4:
return 0.0
p1, p2 = square[0], square[1]
dx = p2[0] - p1[0]
dy = p2[1] - p1[1]
angle = math.degrees(math.atan2(dy, dx))
angle = angle % 90
return angle
def are_squares_different_rotation(self, square1, square2, angle_threshold=10.0):
"""
角度比较也需要考虑90度边界:
角度89度和角度1度在正方形中实际上很相近(差2度)
而不是88度的差距
"""
angle1 = calculate_square_rotation_angle(square1)
angle2 = calculate_square_rotation_angle(square2)
angle_diff = abs(angle1 - angle2)
boundary_diff = min(angle_diff, 90 - angle_diff)
return boundary_diff > angle_threshold
|
1.6 性能优化
像素统计的并行化
在验证正方形质量时,我们需要计算区域内的黑色像素比例。这个操作也可以并行化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| def calculate_square_black_ratio(self, corners):
"""
为什么要并行化像素统计?
对于大的正方形区域,串行计算会很慢
将区域分成上下两部分,并行计算可以提速近一倍
"""
height = self.image_size[1]
mid_y = height // 2
total_pixels_thread1 = 0
black_pixels_thread1 = 0
total_pixels_thread2 = 0
black_pixels_thread2 = 0
def scan_upper_half():
nonlocal total_pixels_thread1, black_pixels_thread1
local_total = 0
local_black = 0
for y in range(0, mid_y):
for x in range(self.image_size[0]):
if mask[y, x] > 0:
local_total += 1
if self.is_black_pixel(x, y):
local_black += 1
with lock:
total_pixels_thread1 = local_total
black_pixels_thread1 = local_black
|
缓存优化策略
在去重过程中,我发现距离计算被重复执行很多次,于是加入了缓存机制:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| def remove_duplicate_corners(self, corners):
"""
缓存设计思路:
距离计算是对称的,distance(A,B) = distance(B,A)
用一个字典缓存计算结果,避免重复计算
"""
distance_cache = {}
def get_distance_cached(p1, p2):
key = (min(p1, p2), max(p1, p2))
if key not in distance_cache:
distance_cache[key] = np.sqrt((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2)
return distance_cache[key]
|
2. 算法性能深度分析
时间复杂度分析
让我们来详细分析一下各个步骤的时间复杂度:
| 前缀和构建 |
O(W×H) |
只需构建一次 |
- |
- |
| 单次区域查询 |
O(1) |
前缀和的核心优势 |
O(W×H) |
O(1) |
| 角点检测 |
O(W×H) |
每个像素检查一次 |
O(W×H×R²) |
O(W×H) |
| 正方形验证 |
O(1) |
固定数量的几何计算 |
O(R²) |
O(1) |
| 总体复杂度 |
O(W×H) |
线性增长 |
O(W×H×R²) |
O(W×H) |
其中W是图像宽度,H是高度,R是检测半径。
空间复杂度分析
1
2
3
4
5
6
7
|
self.image: O(W×H)
self.prefix_sum: O(W×H)
corners: O(N)
distance_cache: O(N²)
|
3. 效果展示
算法在各种测试图像上的识别效果:
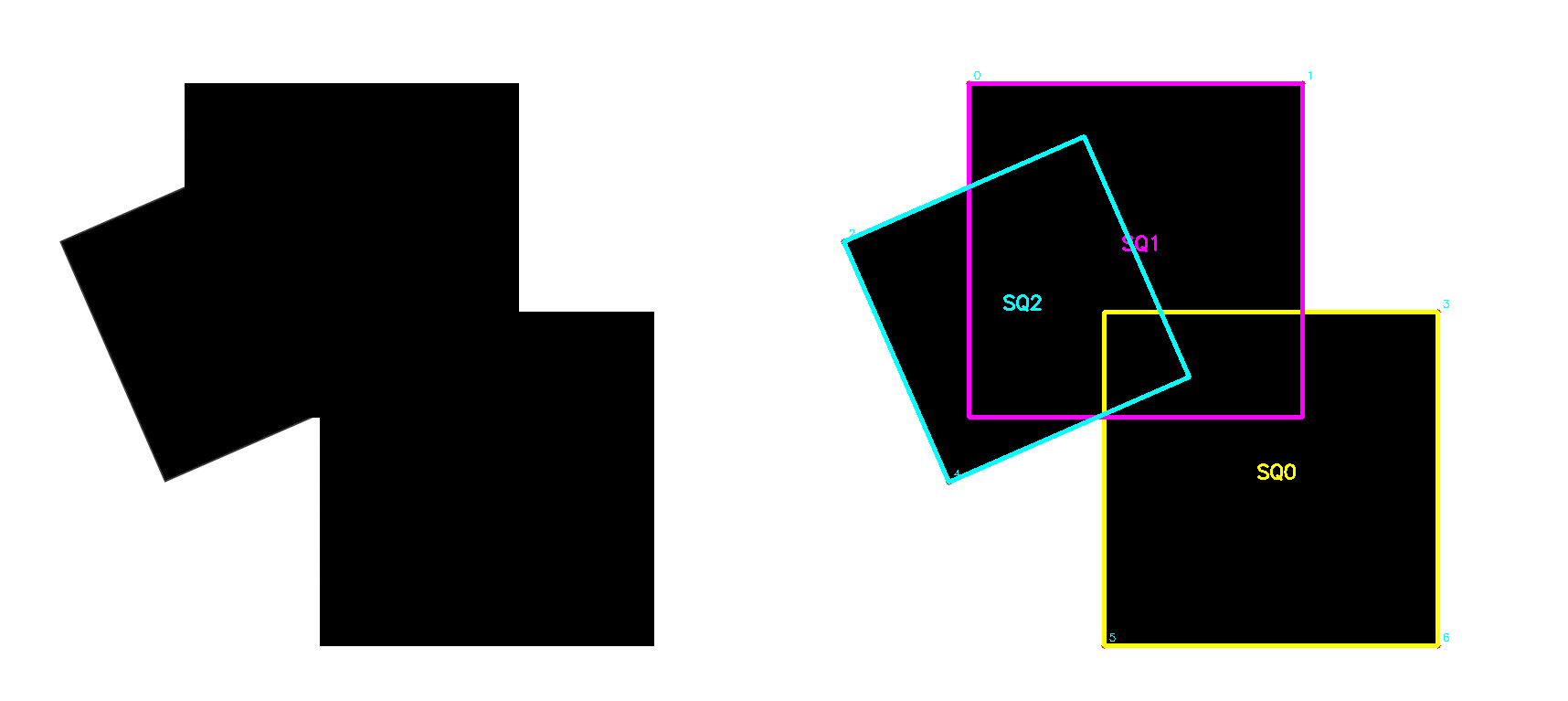



4. 开源和交流
这个项目已经在GitHub上开源:square_recognizer
技术是为了解决实际问题而存在的。希望这个项目和这篇分享能对大家有所帮助。让我们一起在技术的道路上不断前进!

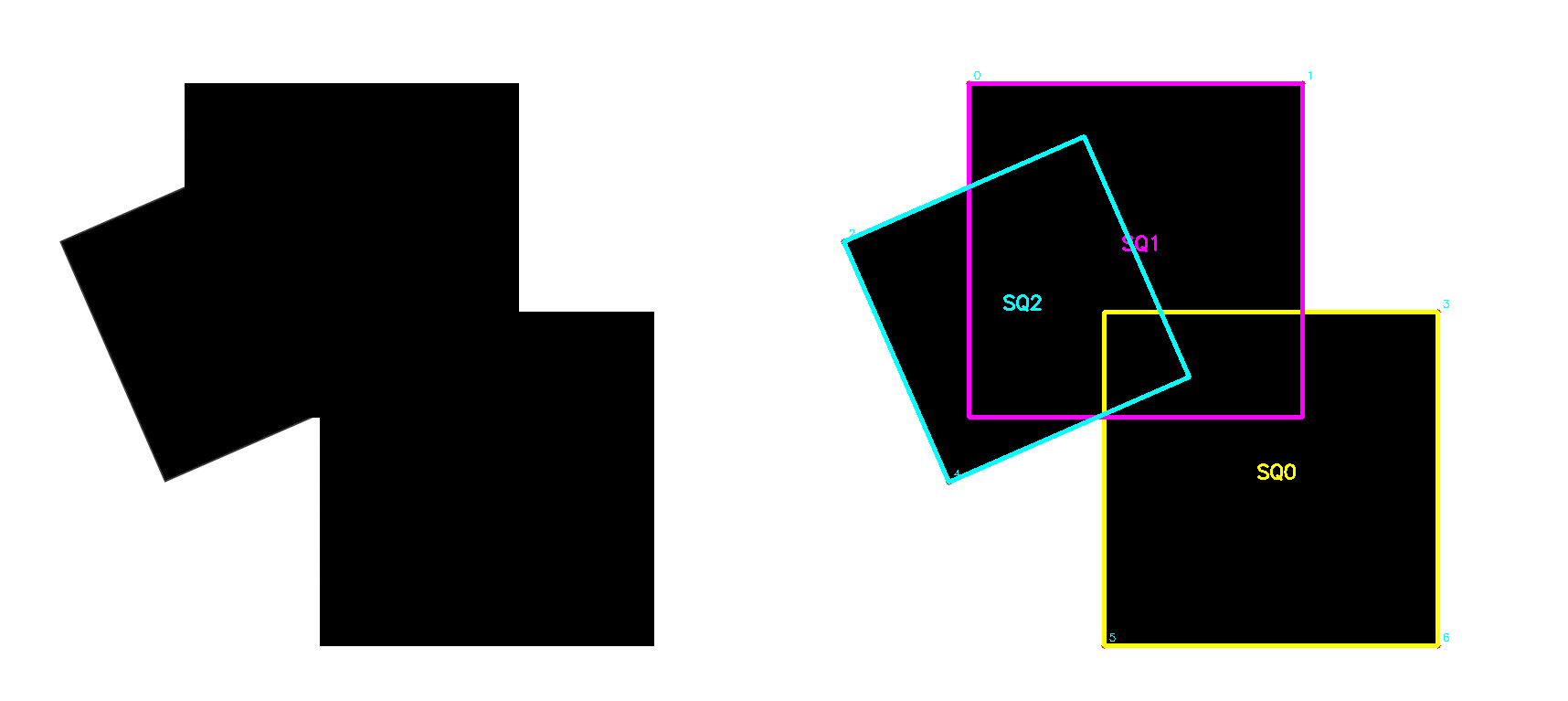








![[COCI 2025/2026 #2] Natjecanje 题解](/img/natjecanje/header.jpg)